XAI_transformers
XAI for Transformers: Better explanations through conservative propagation
Published March 28, 2025
This is a blog post about the article “XAI for Transformers: Better Explanations through Conservative Propagation” published by Ameen Ali et al. in 2022 and available here.
Sure, here is a new version of your article on XAI for Transformers with a more adapted tone:
You’ve probably encountered similar sentences before — they are characteristic of recent language models. These models are built on a specific architecture known as the Transformer, which has extended far beyond Natural Language Processing (NLP) to fields like computer vision, graph analysis, and audio signal processing.
While models relying on Transformers have shown impressive performance, their behavior remains hard to explain, raising questions about their use in sensitive domains like healthcare [1][2], cybersecurity [3][4], recruitment [5] or education [6]. Understanding their decisions therefore becomes a major challenge, to ensure that they do not discriminate on unwanted features (eg. gender, ethnicity).

1. Attribution methods: how to identify important features?
In order to make deep learning models more interpretable, especially in critical applications, it is crucial to understand which input features contribute the most to a model’s prediction. This has given rise to a class of techniques known as attribution methods, whose goal is to assign relevance scores to input features based on their influence on the model’s output.
Formally, consider a function $F: \mathbb{R}^n \rightarrow [0, 1]$ representing a deep network, and an input $x = (x_1, \dots, x_n) \in \mathbb{R}^n$. An attribution of the prediction at input $x$ relative to a baseline input $x'$ is a vector: $A_F(x, x') = (a_1, \dots, a_n) \in \mathbb{R}^n$, where each $a_i$ represents the contribution of feature $x_i$ to the prediction $F(x)$.
Numerous attribution techniques have been proposed, each relying on different strategies to assess feature importance. These methods generally fall into three categories [7]:
- Gradient-based methods: estimate importance using local gradients (e.g., Gradient × Input [8]).
- Perturbation-based methods: assess how the prediction changes when individual input features are modified (e.g., SHAP [9]).
- Attention-based methods: use attention weights to trace how information flows through the model (e.g., Attention Rollout [10]).
While attention-based techniques may appear particularly suitable for Transformers, research has shown that attention weights are not always reliable indicators of feature importance [11][12]. As a result, gradient-based techniques remain among the most widely used approaches, largely due to their computational efficiency compared to perturbation-based techniques. Yet, it's worth noting that these methods were originally designed for simpler architectures, and may not be fully adequate when applied to Transformers.
This brings up a fundamental question: Are existing attribution methods truly suitable for interpreting Transformer models?
A crucial property that any reliable attribution technique should uphold is conservation (also known as completeness) — the principle that the sum of all attributions should match the difference in the model’s output between the actual input and a chosen baseline (a neutral or uninformative input, used as a reference point to isolate the effect of each input feature, such as a black image in image classification tasks).
2. Why conservation is crucial to build XAI?
Without enforcing conservation, attribution-based explanations can become misleading — either by missing important input contributions or by exaggerating the relevance of unimportant ones. This issue is especially critical for complex architectures like Transformers, where components such as attention mechanisms and layer normalization are known to distort the flow of relevance through the network. Rather than proposing a new attribution score, the paper focuses on how to propagate existing attributions through the model in a way that strictly preserves conservation. In other words, the authors study how to ensure that, at each layer of the Transformer, the total relevance is neither lost and not artificially created.
The diagram below shows how different students contributed to a group blog project across three main tasks: content creation, writing, and coding. To evaluate each student’s contribution to the final product, we work backward, tracing the completed blog back to the individual tasks based on their importance, and further attributing each task to the students who contributed. Doing so, we observe that the final result can mainly be attributed to Student 3, while Student 1 and 2 played smaller roles. This backward step-by-step attribution ensures that every contribution is accounted for without any distortion, preventing effort from being lost or exaggerated along the way. This is the idea behind Layer-wise Relevance Propagation (LRP), described in the following part.
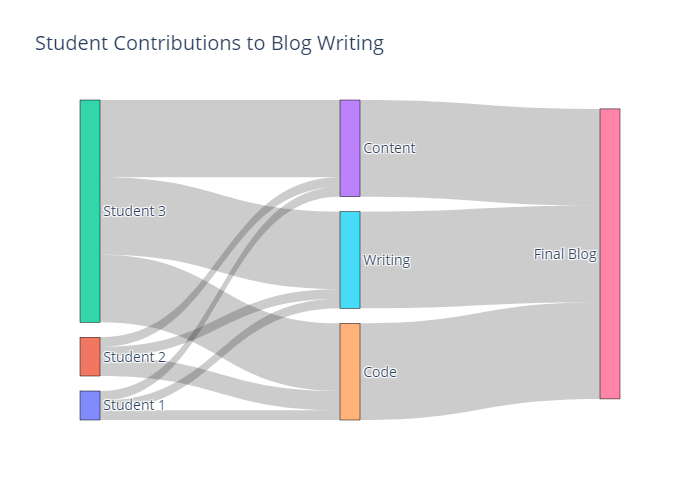
3. Layer-wise Relevance Propagation (LRP) method
Layer-wise Relevance Propagation (LRP) is a method developed to explain the predictions of neural networks by attributing relevance scores to input features. It works by propagating the model’s output backward through the network, redistributing the prediction layer by layer until the input is reached. One of its main advantages is that it satisfies the conservation principle: the total relevance remains constant at each step of the propagation. Originally developed for standard deep neural networks, LRP must be adapted to handle the specific challenges posed by Transformers, such as attention mechanisms. Before addressing these adaptations, let’s first review how the basic version of LRP works.
3.1 Understanding how relevance is propagated and where conservation fails
To understand whether a model satisfies conservation, we must analyze how relevance flows through each layer. The process begins by assigning all the output relevance to the predicted class only. Formally, we define the relevance vector at the final layer $L$, denoted $r_i^{(L)}$, such that:
$$ r_i^{(L)} = \begin{cases} F_i(x) & \text{if } i \text{ is the predicted class}, \\ 0 & \text{otherwise} \end{cases} $$
From there, the relevance is redistributed backward through the network, following specific propagation rules (e.g., LRP-γ, LRP-ε, or LRP-0). One possible rule is the Gradient × Input method, which attributes relevance based on the gradient of the output with respect to each input, scaled by the input itself:
$$ R(x_i) = x_i \frac{\partial f}{\partial x_i}, \quad R(y_j) = y_j \frac{\partial f}{\partial y_j} $$
By applying the chain rule, this becomes:
$$ R(x_i) = \sum_{j} y_j \frac{\partial y_j}{\partial x_i} R(y_j) $$
This formulation allows us to analyze the propagation of relevance and check whether conservation holds at each layer. Specifically, we say that a propagation rule is locally conservative if the sum of relevance scores remains constant from one layer to the next:
$$ \sum_i R(x_i) = \sum_j R(y_j) $$
If this equality is maintained throughout the entire network — from the output all the way back to the input — then the method is said to be globally conservative. When the rule fails to preserve this equality at any layer, we say that conservation breaks, and the explanation becomes less trustworthy.
3.2 Apply directly to transformer architectures?
When applying relevance propagation to Transformer architectures, the conservation principle is not always preserved. The paper identifies two key components where conservation systematically fails and where standard propagation rules require adaptation: Attention Heads and Layer Normalization.
Propagation through Attention Heads:
The figure below illustrates a standard attention head, where relevance \( \mathcal{R}(y) \) is propagated backward through the attention mechanism. This includes a bilinear transformation followed by a softmax over the key-query scores. The authors demonstrate that conservation typically breaks in this setting: some attention heads receive too much relevance, while others are undervalued. This leads to distorted explanations that do not faithfully reflect the model’s true internal computations.
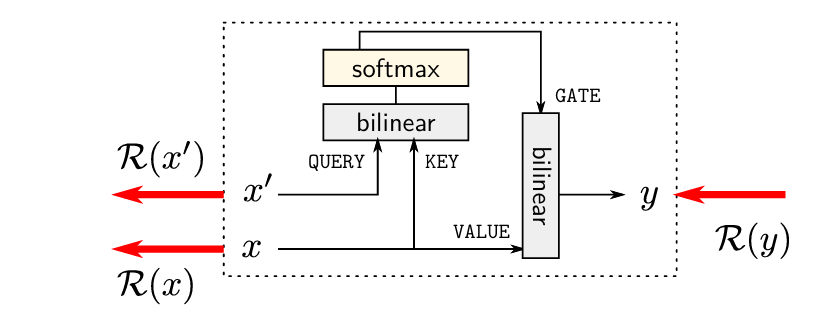
Propagation through Layer Normalization:
In the case of Layer Normalization, the focus is on the centering and scaling operations applied to the inputs. These include subtracting the mean and dividing by the norm of the input — operations that inherently distort the distribution of relevance. The authors show that, regardless of the propagation rule used, conservation is systematically violated when passing through this layer. In other words, relevance is either lost or created during normalization, which undermines the reliability of the explanation.
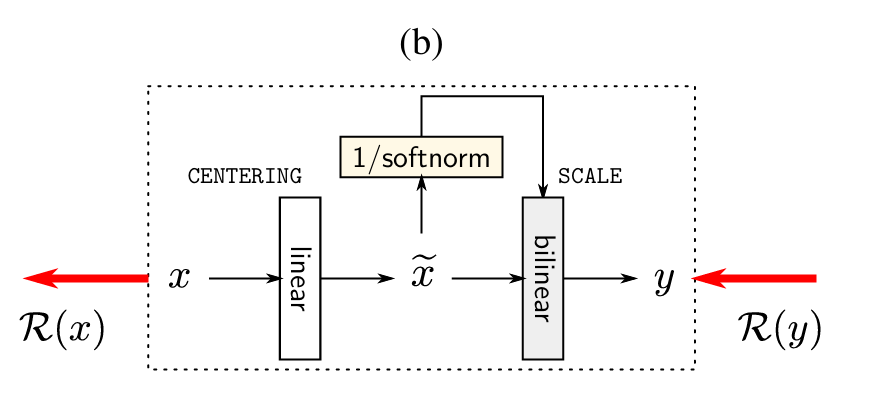
These findings show that classical LRP rules cannot be directly applied to Transformers without modification. Addressing these structural issues is necessary for building explanation methods that preserve conservation and provide trustworthy insights into model behavior.
4. Fixing conservation breaks: a simple but effective trick
To restore conservation in Transformers, the authors propose a solution: instead of redesigning a new attribution method from scratch, they adjust how existing methods are applied by introducing a locally linear approximation of the attention heads and LayerNorm layers. This trick allows them to reuse the rules from LRP while preserving theoretical soundness.
4.1 Locally linear expansion for Attention Heads
During explanation time, the attention mechanism $$ y_j = \sum_i x_i \, p_{ij} $$ is approximated by treating the attention weights \( p_{ij} \) as fixed constants (they normally depend on the input). This means we "freeze" them so that no gradient is propagated through the softmax. The attention head is then seen as a simple linear layer with fixed coefficients, and the relevance can be propagated using the following LRP rule:
$$ \mathcal{R}(x_i) = \sum_j \frac{x_i , p_{ij}}{\sum_{i’} x_{i’} , p_{i’j}} , \mathcal{R}(y_j) \quad \text{(AH-rule)} $$
This linearization not only restores conservation but also simplifies the computation, as no gradients need to flow through the attention scores.
4.2 Locally linear expansion for LayerNorm
LayerNorm applies a normalization step that shifts and scales the input:
$$ y_i = \frac{x_i - \mathbb{E}[x]}{\sqrt{\varepsilon + \mathrm{Var}[x]}} $$
Here too, the trick is to freeze the normalization factor \( \alpha = \frac{1}{\sqrt{\varepsilon + \mathrm{Var}[x]}} \). Once this is done, the transformation becomes linear again, and can be expressed as:
$$ y = \alpha Cx, \quad \text{where} \quad C = I - \frac{1}{N} \mathbf{1}\mathbf{1}^\top $$
The corresponding relevance rule (LN-rule) is then:
$$ \mathcal{R}(x_i) = \sum_j \frac{x_i , C_{ij}}{\sum_{i’} x_{i’} , C_{i’j}} , \mathcal{R}(y_j) \quad \text{(LN-rule)} $$
Freezing these components essentially allows the explanation to bypass their non-linearities, making the relevance propagation both tractable and faithful to the model's internal behavior.
4.3 Implementation made easy
The best part about this method ? This strategy is remarkably simple to implement. In practice, you don’t need to rewrite custom backward rules. All you need to do is freeze the components during the forward pass using the .detach() function in PyTorch. For example:
- Replace \( p_{ij} \) with
p_{ij}.detach()inside attention layers - Freeze \( \sqrt{\varepsilon + \mathrm{Var}[x]} \) in LayerNorm by detaching it
Then, you can run your usual Gradient × Input attribution as usual, except that now, the relevance propagation respects conservation and produces more trustworthy explanations. As a bonus, computation is faster since gradients no longer need to be computed through these detached components.
This implementation trick, though minimal, has a major impact: it transforms Gradient × Input from a noisy, non-conservative method into a principled, conservation-respecting explanation technique for Transformers.
5. Confirmation with Experiments
So, does this new way of propagating relevance through Transformers actually work better? The authors ran a bunch of experiments to find out — and the short answer is: yes, absolutely.
The method (LRP (AH+LN)) was tested against several well-known explanation techniques across a variety of tasks. We're talking about:
- Text classification : movie reviews (IMDB), sentiment tweets, and SST-2
- Image recognition : handwritten digits with MNIST
- Molecular prediction : predicting biochemical properties from molecule data (BACE)
To evaluate how good the explanations were, they looked at two key aspects:
- Quantitative metrics: How well does the explanation match the model’s actual reasoning?
- Qualitative impressions: Are the explanations clear, focused, and free from noise?
5.1 Quantitative Results
For the quantitative evaluation, the authors use AUAC (Area Under the Activation Curve), that measures how well an explanation highlights the most relevant parts of the input, according to the model’s own internal behavior. The AUAC metric is computed from evaluation setups where only the most (or least) relevant parts of the input are kept, to test how well explanations reflect the model's decision-making. In this context, a higher AUAC indicates a more faithful and precise explanation.
| Method | IMDB | SST-2 | BACE | MNIST |
|---|---|---|---|---|
| Random | 0.673 | 0.664 | 0.624 | 0.324 |
| Attention (last) | 0.708 | 0.712 | 0.620 | 0.862 |
| Rollout | 0.738 | 0.713 | 0.653 | 0.358 |
| GAE | 0.872 | 0.821 | 0.675 | 0.426 |
| GI (Gradient × Input) | 0.920 | 0.847 | 0.646 | 0.942 |
| LRP (AH+LN) | 0.939 | 0.908 | 0.707 | 0.948 |
These results show that LRP (AH+LN) not only preserves theoretical properties like conservation, but also translates into superior empirical performance across tasks ranging from sentiment analysis to molecular prediction.
5.2 Qualitative Comparison
Beyond metrics like AUAC, the authors also examine how different explanation methods behave in practice — both on language (SST-2) and vision (MNIST) tasks. In particular, they visualize how each method highlights relevant input features, and compare their interpretability and focus.
On the SST-2 dataset, all methods correctly assign relevance to the words “best” and “virtues” in a positively labeled sentence. However, A-Last overly emphasizes the word “eastwood”, suggesting an undesirable bias toward named entities. In contrast, LRP (AH) and LRP (AH+LN) assign lower relevance such entity tokens and focus more on sentiment-related words — resulting in more robust and generalizable explanations.
On MNIST (Graphormer model), the same pattern holds: LRP (AH+LN) better localizes the relevance onto the digit-containing superpixels, while attention-based methods like Rollout tend to spread relevance into the background. This confirms that the proposed method yields more precise and informative visualizations.
| Method | Interpretability | Focus on Relevant Inputs | Entity/Background Bias |
|---|---|---|---|
| A-Last | Moderate | Moderate | High |
| Rollout | Moderate | Low–Moderate | Moderate |
| GI (Gradient × Input) | High | High | Low |
| LRP (AH) | High | High | Low |
| LRP (AH+LN) (proposed) | Very High | Very High | Very Low |
These qualitative results support the idea that conservation-aware relevance propagation leads to sharper, more focused explanations, and avoids biases toward irrelevant tokens or background noise.
6. Key Takeaway
Interpreting Transformer models is not straightforward — standard attribution methods often fail to accurately trace relevance through components like Attention Heads and LayerNorm. In this blog post, we explored a targeted solution introduced by Ali et al., which consists in approximating these components as locally linear during explanation.
This small conceptual shift restores the conservation of relevance and significantly improves the quality of explanations. The results speak for themselves: more precise, less noisy, and more interpretable relevance maps across a wide range of tasks.
References
[1] Hörst et al. (2023). CellViT: Vision Transformers for Precise Cell Segmentation and Classification. Available here.
[2] Boulanger et al. (2024). Using Structured Health Information for Controlled Generation of Clinical Cases in French. Available here.
[3] Seneviratne et al. (2022). Self-Supervised Vision Transformers for Malware Detection. Available here.
[4] Omar and Shiaeles. (2024). VulDetect: A Novel Technique for Detecting Software Vulnerabilities Using Language Models. Available here.
[5] Aleisa, Monirah Ali; Beloff, Natalia; White, Martin (2023). Implementing AIRM: A new AI recruiting model for the Saudi Arabia labour market, Journal of Innovation and Entrepreneurship. Available here.
[6] Guo, K., Wang, D. (2024) To resist it or to embrace it? Examining ChatGPT’s potential to support teacher feedback in EFL writing. Available here.
[7] Mukund Sundararajan and Ankur Taly and Qiqi Yan (2017) Axiomatic Attribution for Deep Networks. Available here.
[8] Avanti Shrikumar and Peyton Greenside and Anna Shcherbina and Anshul Kundaje (2017) Not Just a Black Box: Learning Important Features Through Propagating Activation Differences. Available here.
[9] Scott Lundberg and Su-In Lee (2017) A Unified Approach to Interpreting Model Predictions. Available here.
[10] Samira Abnar and Willem Zuidema (2020) Quantifying Attention Flow in Transformers. Available here.
[11] Sarthak Jain and Byron C. Wallace (2019) Attention is not Explanation. Available here.
[12] Sofia Serrano and Noah A. Smith (2019) Is Attention Interpretable? Available here.


