NTK-SAP: IMPROVING NEURAL NETWORK PRUNING BY ALIGNING TRAINING DYNAMICS
This is a blog post about the paper NTK-SAP: Improving neural network pruning by aligning training dynamics, published by Y. Wang et al. in 2023 and available here.
Introduction:
In a world increasingly driven by demand for data and computational resources, the narrative of artificial intelligence has been one of abundance: more data, more power, more precision. Yet, nestled within this grand tale, lies a quieter narrative - one that champions the concept of achieving more with less—Frugal AI.
Imagine a craftsman from a bygone era, working in a workshop filled with natural light. Instead of an overwhelming array of tools, he possesses only a few, each worn and refined by years of careful use. With these simple instruments, he creates works of unexpected beauty, demonstrating that the value lies not in the abundance of resources, but in the skill and wisdom with which they are used. Frugal AI embodies this craftsman’s spirit in the digital age. It does not revel in the excesses of computational power or data. Instead, it thrives in constraint, finding clever pathways through the limitations, optimizing algorithms not just for performance, but for efficiency and accessibility.
In the quest for efficiency, neural network pruning has emerged as a foundation of Frugal AI principles. Just as craftsmen meticulously select and refine their tools, neural network pruning systematically removes redundant, non-critical components from a network, optimizing its performance without compromising its functionality.
Neural network pruning
Neural network pruning stems from the recognition that many models, especially deep learning networks, are often over-parameterized. This means they contain more parameters than are necessary for effective learning or inference. In the context of Frugal AI, this over-parameterization is analogous to an artist’s studio cluttered with unused tools and materials, which, rather than aiding, only serve to overwhelm and complicate. The act of pruning, therefore, can be seen as an effort to streamline and refine. It’s about identifying and removing the ’excess’ in the network—those weights and connections that contribute little to the output. This not only reduces the computational load, making the network faster and more energy-efficient, but also often improves its generalization ability, making the model less prone to overfitting and more adaptable to different tasks or datasets.
Pruning Methods:
Pruning methodologies come in various forms, each tailored to specific needs and objectives. These methodologies can be categorized into three main types: post-hoc pruning, pruning during training, and foresight pruning.
Post-hoc Pruning: This technique trims neural networks after training, typically requiring multiple train-prune-retrain cycles. It utilizes various metrics, like magnitude and Hessian values, to determine which weights to eliminate, primarily aiming to reduce inference time.
Pruning During Training: This approach involves gradually removing connections within a neural network as it trains, employing regularization or trainable masks. It aims to save training time but doesn’t necessarily reduce memory costs.
Foresight Pruning: This strategy prunes networks before training begins to prevent unnecessary computational waste. It seeks to address issues like layer collapse collapse at high sparsity levels. Recent advancements aim to overcome the limitations of early pruning methods by incorporating more informed strategies, such as meta-gradients.
Foresight pruning methods - saliency score:
Foresight pruning methods optimize neural network structures by identifying and removing less important connections, reducing computational complexity while maintaining performance. At the heart of these methods lies the loss function, which serves as the guiding metric for evaluating the network’s performance on a given dataset and determining which connections to prune. Given the complexity of directly solving the loss function, an indirect method is employed. Each potential connection within the network is assigned a “saliency score,” reflecting its influence on the loss function. This score is computed by assessing how changes in the connection impact the loss function, scaled by the initial weight value. Essentially, connections with higher saliency scores, indicating greater impact on the loss function, are retained, while those with lower scores are pruned. This systematic approach ensures that the network remains efficient while preserving its effectiveness in solving tasks.
Key pruning methods such as SNIP, Iterative SNIP, GraSP, and Synflow, introduce specific saliency measures to assess the importance of connections:
1. SNIP calculates saliency as $S_{\text{SNIP}}(m’) = \left|\frac{\partial L}{\partial \theta}\odot \theta\right|$, focusing on the impact of each connection on the loss. SNIP’s saliency score is the difference in the loss function before and after pruning a connection.
2. Iterative SNIP repeats the process of SNIP multiple times for a refined pruning.
3. GraSP employs the Hessian-gradient product to identify connections important for preserving gradient flow, with saliency defined as $S_{\text{GraSP}}(m’) = -\left[H(\theta \odot m’; D)\frac{\partial L}{\partial \theta}\right] \odot \theta$.
4. Synflow uses $S_{\text{Synflow}}(m’) = \left|\theta\right| \odot \left|\frac{\partial L}{\partial \theta}\right|$ as a data-agnostic measure, emphasizing connections’ overall contribution to the network’s output irrespective of the dataset.
Each method’s saliency score guides the pruning process by ranking the connections based on their calculated importance to only keep the top-ranked connections - the most salient ones. Therefore, the overall idea is to start with a complex network, score each connection by importance, and keep only the most important connections. This results in a simpler network that is cheaper to train and run but still capable of learning effectively from the data.
Neural Tangent Kernel (NTK):
In recent studies, there has been significant exploration into optimizing neural networks on a global scale. One notable area of focus involves leveraging the neural tangent kernel (NTK) to gain deeper insights into how gradient descent functions within extensive deep neural networks. The NTK spectrum provides valuable information about convergence patterns. Remarkably, researchers have observed that the NTK remains consistent throughout training in sufficiently large DNNs. This suggests that the NTK spectrum could serve as a comprehensive measure for understanding training dynamics.
Neural Tangent Kernel Spectrum-Aware Pruning (NTK-SAP):
Consequently, a novel pruning approach has emerged: selectively removing connections that exert minimal influence on the NTK spectrum.
In order to implement this conceptual pruning methods, there are a few considerations:
1. Metric Selection: Due to the complexity and time required to calculate the full range of eigenvalues (the eigenspectrum) of the Neural Tangent Kernel, the nuclear norm—essentially the sum of these eigenvalues—is used instead as a scalar to summarize the characteristics of the eigenspectrum.
2. Choosing the Right NTK Matrix:
We can distinguish between wo types of NTK matrices:
- Fixed-Weight NTK: Related to the network’s initial setup.
- Analytic NTK: A theoretical model assuming a network of infinite size
However, since calculating the Analytic NTK is highly resource-intensive, the researchers use a practical workaround. They approximate the Analytic NTK by averaging multiple Fixed-Weight NTKs from various initial setups, balancing computational efficiency with accuracy.
3. Computational Efficiency: To manage computation costs, there is a technique known as the “new-input-new-weight” (NINW) method. This approach involves changing the network’s weights for each new set of input data. By doing this, they can efficiently evaluate the properties of the Neural Tangent Kernel (NTK) across different scenarios without significantly adding to the computational load.
Based on these considerations, Wang and colleagues have developed an innovative approach called Neural Tangent Kernel Spectrum-Aware Pruning (NTK-SAP).
NTK-SAP leverages the NTK spectrum for efficient foresight pruning by using multi-sampling to predict pruning outcomes and ensure accuracy. It also incorporates the Novel Iterative Network Weighting (NINW) technique to reduce computation costs. This method streamlines neural networks by preemptively removing less impactful parts, optimizing both the pruning process and the network’s performance with minimal resource expenditure.
NTK-SAP follows the following implementation:

Calculation of NTK-SAP Saliency Score:
1. Finite Approximation Approach
The NTK-SAP method introduces a finite approximation expression to calculate a saliency score S-NTK-SA, which leverages the pruning dataset to approximate the entire training set. This foresight pruning approach identifies and prunes weights with the lowest saliency scores.
Saliency score based on a fixed-weight Neural Tangent Kernel:
$$S_{\text{NTK-SAP}}(m^j) = \left| \frac{\partial}{\partial m_j} \mathbb{E}_{\Delta\theta \sim \mathcal{N}(0, \epsilon I)} \left[ \left| f(\mathbf{X}_D; \theta_0 \odot m) - f(\mathbf{X}_D; (\theta_0 + \Delta\theta) \odot m) \right|_2^2 \right] \right|$$
2. Multi-Sampling Approach:
While a single fixed-weight-NTK provides an approximation of the analytic NTK, averaging over multiple fixed-weight-NTKs offers a closer approximation to the expected behavior of the analytic NTK. This method entails sampling several independent weight configurations and averaging their fixed-weight-NTKs to better understand the parameter space and the anticipated performance of pruned networks.
A stabilized version of the saliency score, S-NTK-SAP(mj) is introduced and incorporates the average of fixed-weight-NTKs computed across multiple random weight configurations, to assess the impact of pruning. Unlike most existing foresight pruning scores, which are dependent on specific weight configurations, this proposed saliency score is weight-agnostic; it primarily reflects the structure of the mask applied for pruning rather than the weights themselves. This distinction highlights the score’s focus on the inherent characteristics of the pruning method over the variability of weight initializations.
3. New-input-new-weight (NINW) trick:
To reconcile the theoretical aspirations with practical viability, NTK-SAP leverage the ’new-input-new-weight’ (NINW) trick. This technique estimates the expected behavior of pruned networks by utilizing a new set of weights for each mini-batch of input data. This approach ensures that the pruning algorithm remains computationally feasible, allowing for the real-world application without prohibitive resource demands.
4. Random Input Trick:
NTK-SAP relies on another trick that consists in replacing the pruning set with random inputs. This allows to approximate the network’s behavior without depending on real data, thus highlighting NTK-SAP’s ability to adapt to any dataset without requiring specific adjustments or optimization.
$$S_{\text{NTK-SAP}}(m^j) = \left| \frac{\partial}{\partial m_j} \frac{1}{|D|} \sum_{i=1}^{|D|} \left[ \left| f\left(Z_i; \theta_{0,i} \odot m\right) - f\left(Z_i; \left(\theta_{0,i} + \Delta\theta_i\right) \odot m\right) \right|_2^2 \right] \right|$$
Experimental validation:
Experiments were performed on CIFAR-10, CIFAR-100, and Tiny-ImageNet data sets to validate NTK-SAP’s superiority across various sparsity levels. Particularly noteworthy is its robust performance at extreme sparsity ratios, where traditional methods falter. These results underscore the efficacy of our multi-sampling strategy and the practical utility of the NINW trick.
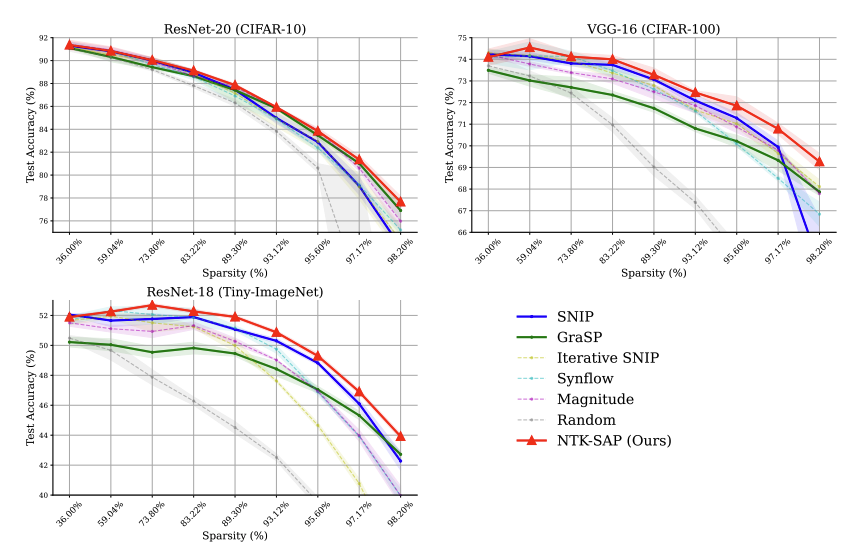
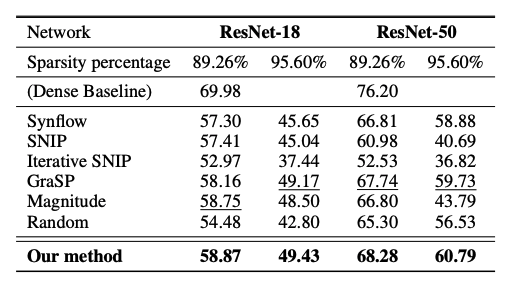
Extending the analysis to the more challenging ImageNet dataset, NTK-SAP consistently outperforms baseline pruning methods, including SNIP and GraSP, especially at high sparsity levels. This success highlights NTK-SAP’s scalability and its potential to facilitate efficient neural network training on large-scale datasets.
Reproductive experiments:
To ensure reproducibility, begin by installing the required packages:
pip install -r requirements.txt
Next, to run NTK-SAP with the default dataset and parameters using the following command:
python main.py
The default parameters are as follows:
--dataset: Mnist--model-class: default--model: fc--pruner: rand--prune-batch-size: 256--compression: 0.0--prune-train-mode: False--prune-epochs: 1--ntksap_R: 1--ntk_epsilon: 0.01
For experimenting with different parameters, proceed with the desired adjustments.
1. Experiment NTK-SAP with Cifar100 dataset, a 0.01 perturbation hyper-parameter
python main.py --dataset cifar100 --ntksap_epsilon 0.01
Train results:
| train_loss | test_loss | top1_accuracy | top5_accuracy | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Init. | 0 | NaN | 4.607083 | 1.00 | 4.96 | ||||
| Pre-Prune | 0 | NaN | 4.607083 | 1.00 | 4.96 | ||||
| Post-Prune | 0 | NaN | 4.607083 | 1.00 | 4.96 | ||||
| Final | 10 | 3.337817 | 3.421804 | 17.91 | 45.41 |
2. Experiment NTK-SAP with Cifar100 dataset and a 0.02 perturbation hyper-parameter
python main.py --dataset cifar100 --ntksap_epsilon 0.02
Train results:
| train_loss | test_loss | top1_accuracy | top5_accuracy | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Init. | 0 | NaN | 4.607163 | 1.02 | 4.72 | ||||
| Pre-Prune | 0 | NaN | 4.607163 | 1.02 | 4.72 | ||||
| Post-Prune | 0 | NaN | 4.607163 | 1.02 | 4.72 | ||||
| Final | 10 | 3.341863 | 3.460254 | 17.74 | 43.78 |
3. Experiment NTK-SAP with Cifar100 dataset and a number of iterations of 3
python main.py --dataset cifar100 --prune-epochs 3
Train results:
| train_loss | test_loss | top1_accuracy | top5_accuracy | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Init. | 0 | NaN | 4.606948 | 0.96 | 5.02 | ||||
| Pre-Prune | 0 | NaN | 4.606948 | 0.96 | 5.02 | ||||
| Post-Prune | 0 | NaN | 4.606948 | 0.96 | 5.02 | ||||
| Final | 10 | 3.337061 | 3.448972 | 18.09 | 43.97 |
4. Experiment NTK-SAP with Cifar100 dataset and a number of iterations of 7
Train results:
| train_loss | test_loss | top1_accuracy | top5_accuracy | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Init. | 0 | NaN | 4.606786 | 1.01 | 4.95 | ||||
| Pre-Prune | 0 | NaN | 4.606786 | 1.01 | 4.95 | ||||
| Post-Prune | 0 | NaN | 4.606786 | 1.01 | 4.95 | ||||
| Final | 10 | 3.335409 | 3.397401 | 18.93 | 44.89 |
Analysis from experiments:
1. Dataset Adaptability:
The study demonstrated NTK-SAP as being data-free. This quality allows pruned networks developed via these methods to be seamlessly adapted to various datasets without requiring additional data, highlighting their versatility and efficiency.
2. Robustness across hyper-parameter variations:
The robustness of NTK-SAPP is evident through its consistent performance across varying perturbation hyper-parameters (ϵ) in experiments conducted on the Cifar100 dataset. When the perturbation hyper-parameter is set to 0.01, the model exhibits stable behavior throughout training and pruning phases, yielding a final top-1 accuracy of 17.91% and a top-5 accuracy of 45.41%. Similarly, when the perturbation hyper-parameter is increased to 0.02, the model maintains its stability, with minimal fluctuations observed in performance metrics compared to the unperturbed model. Both pre-prune and post-prune stages demonstrate resilience to perturbations, showcasing nearly identical results to the unperturbed model. This consistency across different perturbation levels underscores the robustness of NTK-SAPP, making it a reliable choice for tasks where stability under varying conditions is crucial.
3. Fewer iterations for small datasets:
An exploration into how the number of iterations (T) affects performance across datasets reveals that for smaller datasets, reducing T slightly impacts outcomes, suggesting that computational efficiency can be achieved without significantly compromising results.
Conclusion:
In conclusion, NTK-SAP stands as a pivotal advancement in the realm of neural network pruning, showcasing its efficacy across diverse datasets and network architectures. By pruning at initialization, it eliminates the necessity for post-training methods and mask training. Moreover, by leveraging NTK theory, it addresses the oversight of training dynamics post-pruning, enabling iterative pruning without data dependency. NTK-SAP effectively bridges the theoretical underpinnings of optimization with practical neural network training, thus pushing the boundaries of frugal neural networks.
While NTK-SAP represents a significant leap forward, it also unveils several avenues for future exploration. Subsequent research could delve into alternative spectral measures or extend the methodology to other forms of network optimization.
In essence, NTK-SAP not only signifies a crucial stride towards more efficient and theoretically grounded neural network pruning but also sets the stage for future innovations in enhancing network frugality.
By Elia Lejzerowicz and Adrien Oleksiak.